Spectre d'émission de l'hydrogène

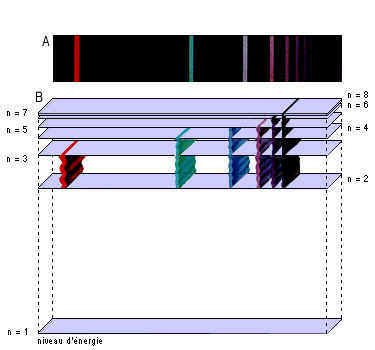
N. B. : Balmer identifia 4 raies dans le spectre visible de l'hydrogène, situées à des longueurs d'onde de 656,3 nm, 486,1 nm, 434,0 nm et 410,2 nm, et les nomma respectivement Ha, Hb, Hg et Hd. En 1885, il établit que ces quatre longueurs d'onde l, appelées depuis série de Balmer, pouvaient s'exprimer par la formule : l!=!B!n²!/!n²!-!4 où n est un entier égal à 3, 4, 5 ou 6, et B une constante.

En 1889, le physicien suédois Rydberg découvrit une écriture simplifiée de cette formule sous la forme : s !=!1!/!l!=!R_H!(1/2²!-!1!/!n²) où s est le nombre d'onde et R_H la constante de Rydberg associée à l'hydrogène.

En 1913, Bohr déduisit une formule générale relative aux raies du spectre de l'hydrogène. Cette formule donnait entre autres les longueurs d'onde des raies de Balmer. Elle s'écrit : 1!/!l!=!R_H!(1!/!k²!-!1!/!n²) où k et n sont des entiers non nuls. Si k = 2, on retrouve la formule de Balmer, qui correspond aux transitions des électrons des orbites supérieures vers la deuxième orbite. Si k = 1, on obtient la série des raies dans l'ultraviolet, dite série de Lyman, relative aux transitions électroniques vers l'orbite la plus basse. D'autres séries de raies dans l'infrarouge comme celles de Paschen, de Brackett et de Pfund sont associées respectivement aux valeurs k = 3, 4 et 5.